In computer science, a quine is a computer program which outputs a copy of its own source code. (See the Wikipedia page on quines for more information and examples.) I recently discovered a different sort of quine: mathematical ones.
Consider the function \[{1\over 2} < \left\lfloor \mathrm{mod}\left(\left\lfloor {y \over 17} \right\rfloor 2^{-17 \lfloor x \rfloor – \mathrm{mod}(\lfloor y\rfloor, 17)},2\right)\right\rfloor\]
where
- \(\lfloor x \rfloor\) is the floor function, i.e. the largest integer less than \(x\);
- \(\bmod(b,m)\) is the modulo operation, which, when graphed over \(0\leq x\leq 106\) and \(n\leq y\leq n+17\) with n = 4 858 450 636 189 713 423 582 095 962 494 202 044 581 400 587 983 244 549 483 093 085 061 934 704 708 809 928 450 644 769 865 524 364 849 997 247 024 915 119 110 411 605 739 177 407 856 919 754 326 571 855 442 057 210 445 735 883 681 829 823 754 139 634 338 225 199 452 191 651 284 348 332 905 131 193 199 953 502 413 758 765 239 264 874 613 394 906 870 130 562 295 813 219 481 113 685 339 535 565 290 850 023 875 092 856 892 694 555 974 281 546 386 510 730 049 106 723 058 933 586 052 544 096 664 351 265 349 363 643 957 125 565 695 936 815 184 334 857 605 266 940 161 251 266 951 421 550 539 554 519 153 785 457 525 756 590 740 540 157 929 001 765 967 965 480 064 427 829 131 488 548 259 914 721 248 506 352 686 630 476 300.
This is known as Tupper’s Formula (created by Jeff Tupper in 2001). It produces the following “graph”.
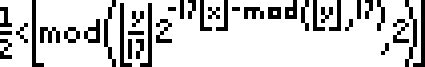
If you look closely, this graph is a bitmap which has been chosen out of all possible bitmaps of this size by the value of \(n\) specified above, making it not truly self-referential. A real (and complex) self-referential mathematical formula was created by Jakub Trávník earlier this year.
